Zenna Tavares

Computer Assisted Programming Group (PI: Armando Solar Lezama)
Department of Brain and Cognitive Sciences
CSAIL

JuliaCon 6/25/2015

What is Probabilistic Programming?



J Jara-Ettinger, L Schulz, JB Tenenbaum (2015).


Example: Inverse Planning

Parameter Estimation

Infer rate parameter of exponential distribution

$$ \begin{split} \lambda &\sim \mathrm{Uniform}(0, 2)\\ x_n &\sim \mathrm{Exponential}(λ)\\ observe \; \mathbf{x} &= [0.083, 0.55, 2.37]\\ \end{split} $$

Conditional Samples


prior
posterior

Inference Queries

Conditional sampling with rand

λ = uniform(0,2)
x1 = exponential(λ)
x2 = exponential(λ)
x3 = exponential(λ)
observations = (x1 == 0.083) & (x2 == 0.55) & (x3 == 2.37)

rand(λ, observations, 100)

Conditional Sampling is Not Easy

probability of observation == true becomes vanishingly small

dream
reality

Random Variables are not Random!

They are functions

λ = uniform(0,2)
typeof(λ) => RandVar{Float64}

function λ(ω) = ω * 2 end  # input ω ∈ [0, 1]

λ(0.1) => 0.2  # x is just a function

λ = randunif()
λ(ω) => 0.6923295214 # to sample: call with uniformly sampled input

Pointwise Random Variable Algebra

$$ \begin{split} Z &= X + Y\\ Z(\omega) &= X(\omega) + Y(\omega) \end{split} $$

Pointwise Random Variable Algebra

a = exponential(0.5); b = exponential(0.5)
c = a + b
typeof(c) => RandVar{Float64}
rand(c, 5) => [3.425, 2.990, 9.670, 0.45759, 3.6357] 

d = c + 100
typeof(d) => RandVar{Float64}
rand(d, 5) => [104.883, 103.50, 100.50, 100.485, 100.549]

e = exponential(d)
typeof(e) => RandVar{Float64}
rand(e, 5) => [0.020, 0.0043, 0.00108, 0.0041, 0.0052]

Single Sample Space

Random Variables are dependent through \(\Omega\) (Euclidean unit cube)

Single Sample Space

Random Variables are dependent through \(\Omega\) (Euclidean unit cube)

Single Sample Space

Random Variables are dependent through \(\Omega\) (Euclidean unit cube)

Complete Example using Random Arrays

are arrays of RandVars

rand(X::RandVar{T}, Y::RandVar{Bool}, n::Integer) = ...

type RandArray{T,N} <: DenseArray{RandVar{T},N} ...

λ = uniform(0,2)
x = mvexponential(λ, 3)
observations = x == [0.083, 0.55, 2.37]

rand(x, observations, 100)

Demo

Under The Hood

Conditional Inference by Constraint Solving

Single Sample Space

Random Variables are dependent through \(\Omega\) (Euclidean unit cube)

Conditional Sampling is Easy

Guess (probabilistically) and check until condition is satisfied

$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$ 
function rand(X::RandVar, Y::RandVar{Bool})
  while true
    ω = rand_unif_vector()
    if Y(ω)
      return X(ω)
    end
  end
end

Conditional Sampling is Easy

Guess (probabilistically) and check until condition is satisfied

$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$ 
function rand(X::RandVar, Y::RandVar{Bool})
  while true
    ω = rand_unif_vector()
    if Y(ω)
      return X(ω)
    end
  end
end

Conditional Sampling is Not Easy

probability Y(ω) == true becomes vanishingly small

dream
reality

Consider sets instead of single points

and let an Oracle (constraint solver) do the hard work

$$ \mathcal{O}_Y(A) = \left\{ \begin{array}{lr} T & : A \subseteq Y\\ F & : A \cap Y = \varnothing\\ TF & : Otherwise\\ \end{array} \right. $$

Play a game with the Oracle

Split and randomly choose one side

δ-Relaxation

Make thin lines thick - (S Gao, J Avidad, EM Clarke - 2012)

\(Y=X\)
\(Y-X<\delta\)

Example: Geometric Sampling

Sample from surface/interior of geometric objects

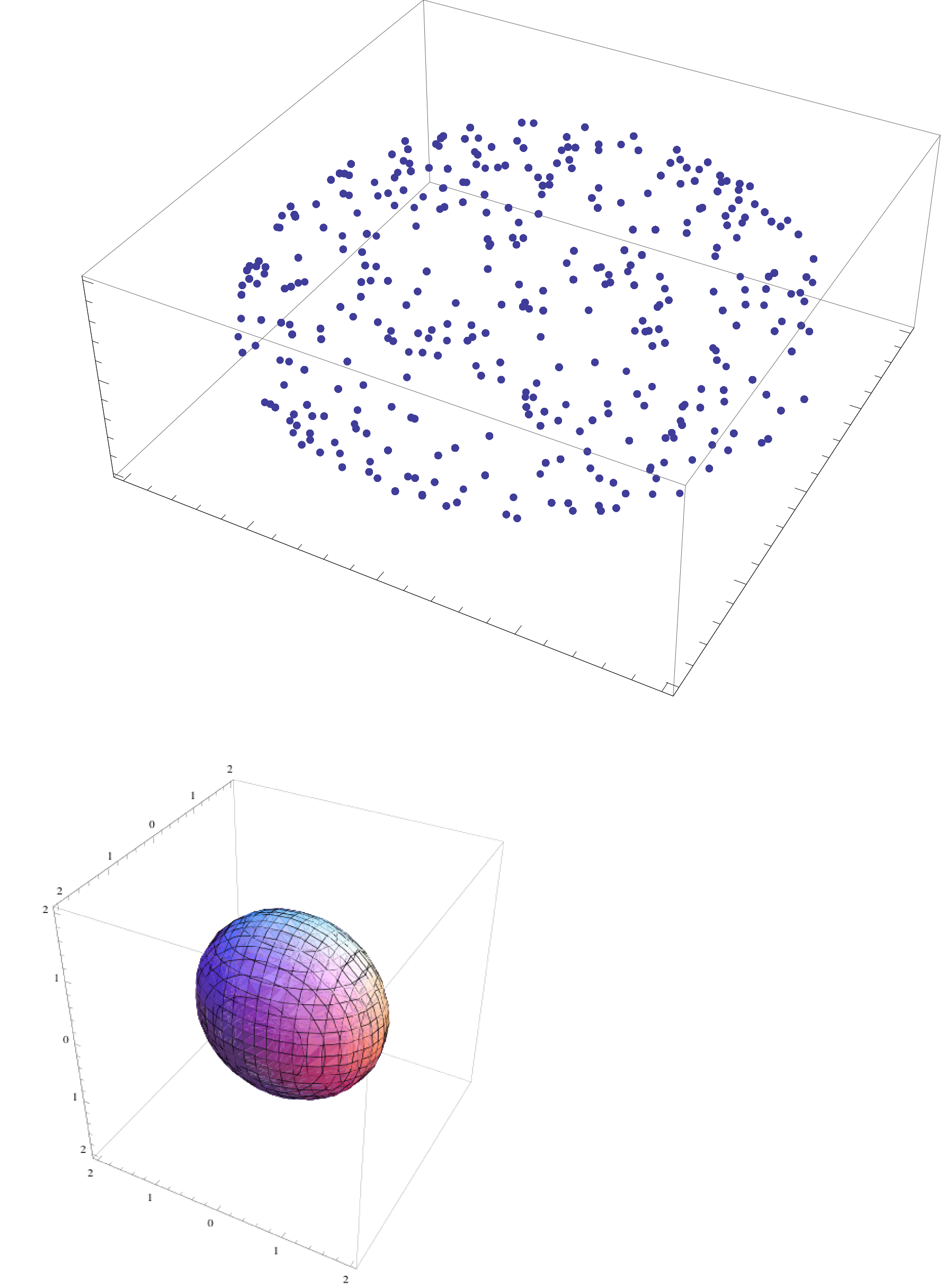
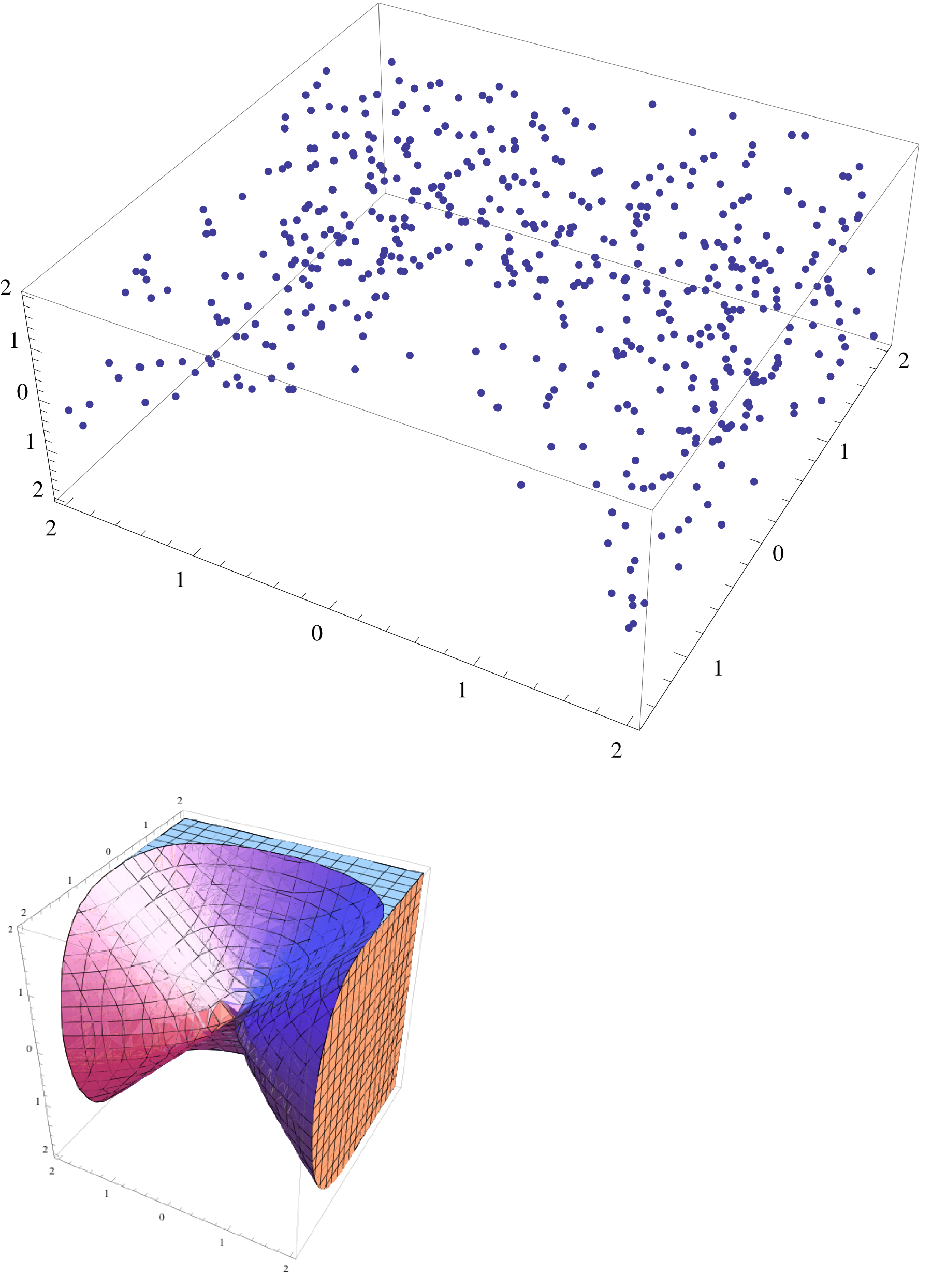
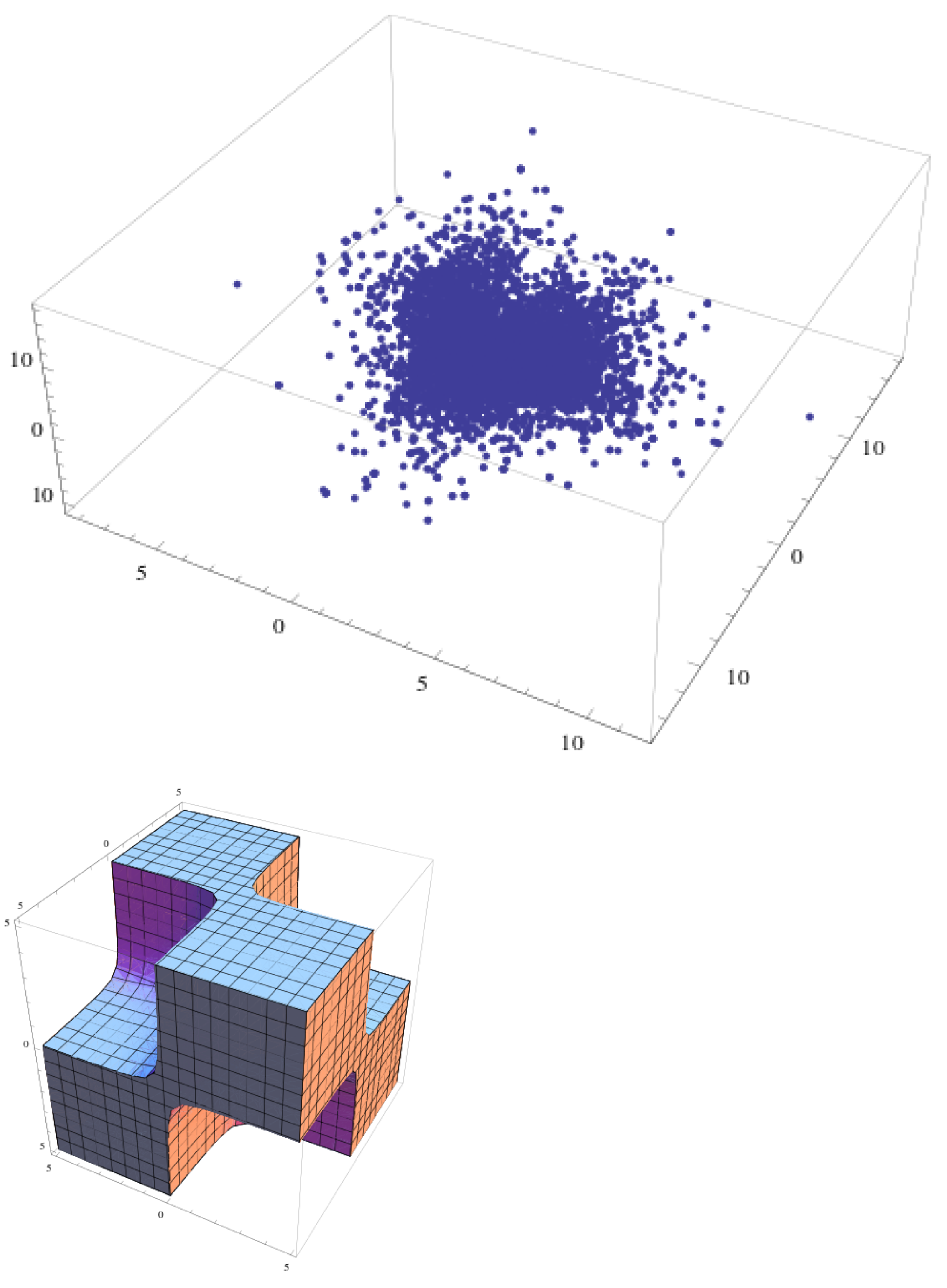
Sigma and Julia

The Good

  • simplicity: model-algorithm separated
  • type hierarchy: use RandVars in existing code
  • runtime compilation

The Ugly

  • types: RandVar{Float64} <: FloatingPoint ?
  • control flow breaks things: if, while, for, &, |, ...

Conclusion

What is Probabilistic Programming?

  • Bayesian and Conditional Inference are same-same but different
  • Sigma is requires complete model - no black boxes
  • One algorithm to rule them all?

Do we need new languages?

  • Not really, no
  • Maybe... Uncertain type Inference? Probabilistic parsing?

Thank You!

Contributors Welcome! - https://github.com/zenna/Sigma.jl